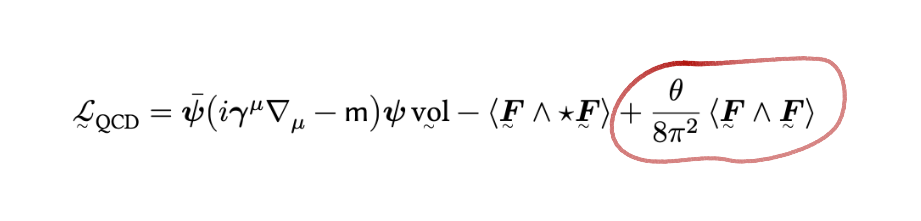Jollywatt blog ⊕ portfolio
World Flags Quizzer
A game to teach you world flags. 🇨🇳🇮🇳🇺🇸🇮🇩🇵🇰🇧🇷🇳🇬🇧🇩⋯ Read more
A Simple Example of a Connection With Torsion
While learning general relativity as an undergrad, I was uneasy with the idea of torsion of an affine connection. Familiar phrases like “torsion measures how a frame twists as it undergoes parallel transport” seemed too lofty to serve as a helpful mental model. The following example is one which gave... Read more
Timeline of Scientists
Interactive timeline of famous scientists throughout history, using Wikidata. Read more
Explicit Baker–Campbell–Hausdorff–Dynkin formula for Spacetime via Geometric Algebra · arχiv
In brief. In \(≤4\) dimensions, there’s a simple formula for the bivector \(σ_3\) in terms of bivectors \(σ_1\) and \(σ_2\) such that \(e^{σ_1}e^{σ_2} = ±e^{σ_3}\). Abstract. We present a compact Baker–Campbell–Hausdorff–Dynkin formula for the composition of Lorentz transformations \(e^{σ_i}\) in the spin representation (a.k.a. Lorentz rotors) in terms of their... Read more
Mathematical One-liners
A collection of succinct but wonderfully satisfying mathematical results. Read more
Light installation for Gatherings Restaurant
Projector light show made for a multi-sensory dining experience. Read more
An Overview of the Strong CP Problem and Axion Cosmology · PDF
Literature review supervised by Dr. Jenni Adams at the University of Canterbury. I wanted to learn more about particle physics after my Bachelor’s, so a year of part-time study culminated in this literature review. I learned basic classical (and a little quantum) field theory, and read about the “strong \(CP\)... Read more
The Many Faces of Stokes’ Theorem
Interactively tabulate the special cases of Stokes’ theorem, \( \int_Ω \dd ω = \int_{∂Ω} ω \). Read more